A Level Chemistry Revision: Physical Chemistry – Equilibrium Constant Kp For Homogeneous Systems

Analysing the chemical reactions of gases in homogeneous systems may seem daunting at first. Unlike a liquid solution, the volume of gas isn’t constant, so determining the concentration of specific gas reactants is difficult when you base it on volume. This is where the concepts related to the equilibrium constant K_p for homogeneous systems of gases come into play.

However, before you proceed with revising this topic, it’s important that you first understand K_c (the constant of concentration in liquid systems), as well as the concept of dynamic equilibrium, and Le Chatelier’s Principle. All of these concepts are related to the equilibrium constant K_p. 

What is Dynamic Equilibrium?

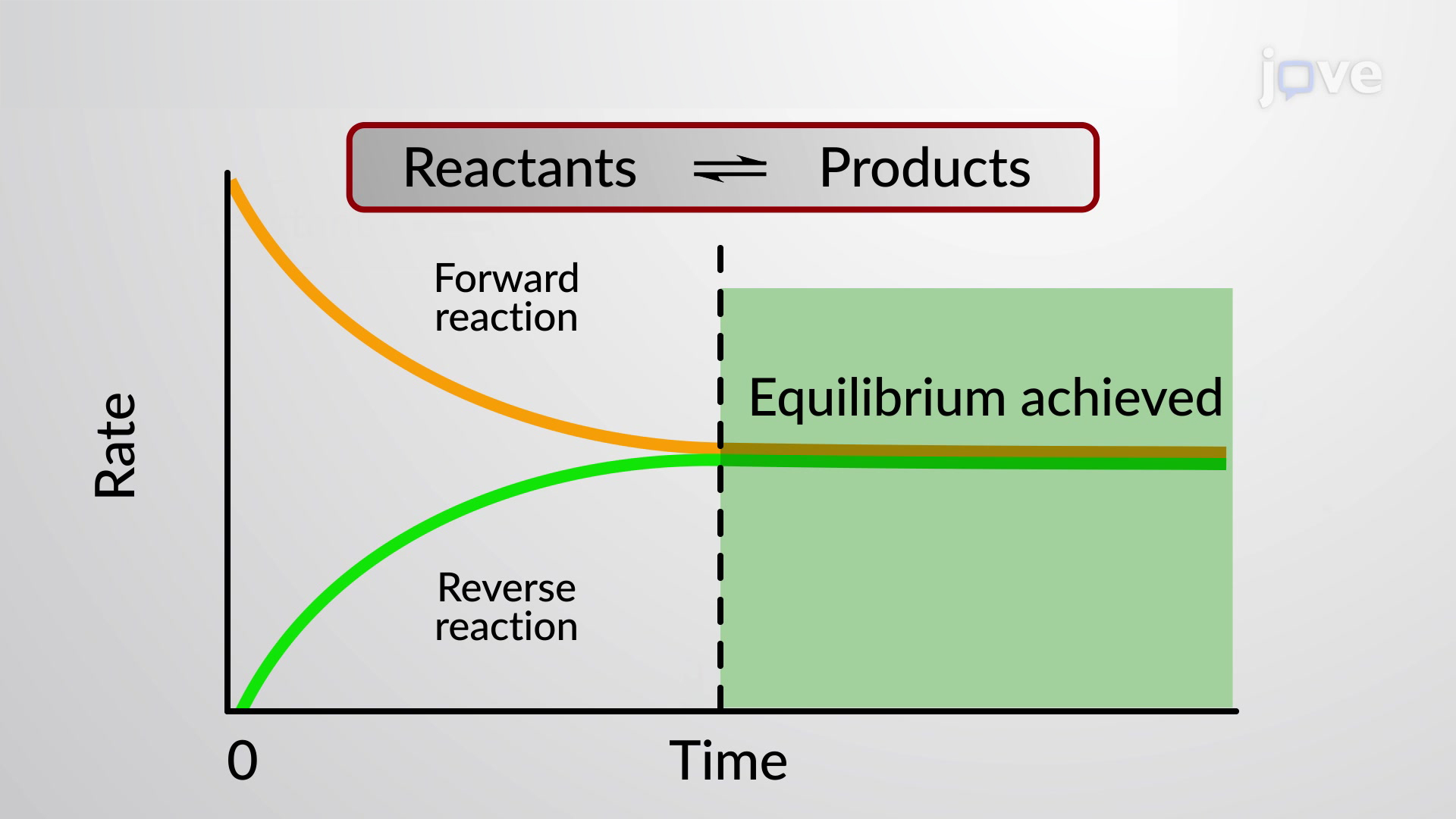
When we talk about equilibrium in chemistry, we’re more interested in dynamic equilibrium rather than static equilibrium. Dynamic equilibrium refers to a chemical system in which both the forward and reverse reactions are continuous, but have attained a level of equilibrium or balance.

Although all chemical reactions are conceptually reversible, many are almost impossible to reverse because of entropy and the need for higher energy or complex processes. For example, if you burn paper, it would be practically impossible to reconstitute its cellulose components from the ashes and carbon dioxide. Therefore, dynamic equilibrium is applicable only to reactions that are practically reversible.

Reversible chemical reactions in dynamic equilibrium are typically written with forward and backward half arrows, as shown in the equation below, which describes the reversible decomposition reaction of colourless dinitrogen tetroxide into brown nitrogen dioxide, and vice versa:What is the Le Chatelier’s Principle?

Le Chatelier’s Principle is named after Henry Le Chatelier, who first published the principle in 1888, though it was also independently discovered by Karl Ferdinand Braun. The principle can be stated as follows:

“In any chemical system in equilibrium, the introduction of change in concentration, temperature, volume, or pressure, will shift the equilibrium to counteract the change.”

This means that the equilibrium can shift either to the left or to the right. An important thing to remember is that at equilibrium, the concentration of reactants and products are not necessarily equal.

What’s the Difference Between K_c and K_p?

K_c and K_p are mathematically similar. They both represent the proportions between reactants and products, and refer to the dynamic equilibrium state between the reactants and products. The generalised balanced reversible reaction below is the basis of the two constants. The lowercase letters represent the coefficients, while the uppercase letters represent the chemical species:

The main difference between the two constants is the parameters they represent. K_c represents the concentration constant, while K_p represents the pressure constant. As you can see below, K_c has square brackets around the chemical species. In the exam, you should always use the square brackets to indicate concentrations.

Meanwhile, the K_p equation represents pressure instead of concentration. This is denoted by a lowercase ‘p’ and the parentheses. The lowercase ‘p’ that precedes every chemical species in parentheses represents the partial pressure of that particular chemical species. However, similar to  K_c, the exponents represent molarity:

The  K_p equation is for homogenous gas systems. Since gases don’t have definite volume and they’re dependent on their container, pressure is the appropriate parameter to equate with molarity.

What is Partial Pressure?

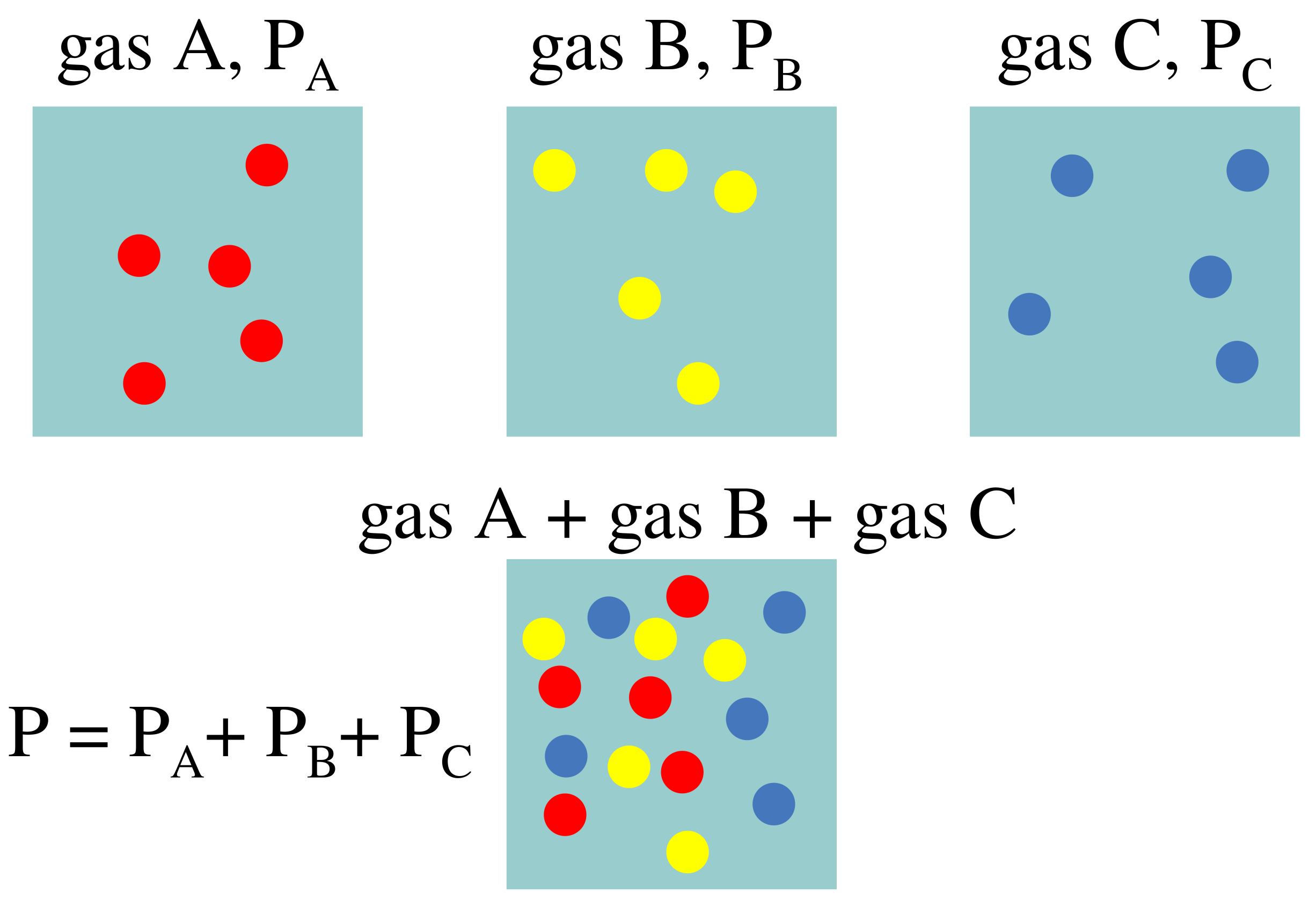
Homogeneous gas mixtures exert an overall pressure on their containers that is the sum of the partial pressures of the individual gases inside. The partial pressures are directly proportional to the number of particles or moles of the gas. This gas behaviour was empirically discovered by John Dalton in 1801.

Dalton’s Law of gases is stated as follows:

“In a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases.”

As shown in the schematic diagram below, individual gases exert respective partial pressures. The partial pressures can either be equal or unequal to each other.

What is Mole Fraction?

Mole fractions are the proportions of constituent substance in a homogeneous mixture. They’re basically just the ratio between the mole of a gas in a mixture and the total number of moles of all other substances in the mixture. The equation demonstrates how the mole fraction of a gas is computed:

Using the K_p formula, you can calculate the partial pressure and the mole fraction of a given gas in a mixture. In your exam, you’ll encounter problems that will ask you to calculate unknown variables. When you do this, you need to be skillful in your algebra manipulations of the equations. Let’s examine the sample problem below and apply the mole fraction and K_p formulas:

Applying the mole fraction formula, we get the following answer:

X_A = 0.14 mol/(0.52 mol + 0.01 mol)

X_A = 0.21

The mole units will cancel out, leaving only the decimal figure. This is the same as 21%, which is the proportion of oxygen in the air.

An important constant to remember is the Avogadro’s number, which is the total number of the unit particles of a substance (atoms or molecules) in one mole of that substance. It can be written as 6.022 x 10²³.

Remember that the more particles a gas has, the greater its partial pressure. This means that partial pressure can be calculated based on the molar fraction of a gas, and vice versa, under specific conditions. Here’s an example:

If the total pressure and the mole fraction are known, but the individual partial pressure of each gas in a mixture is unknown, you can calculate this using the formula above.

In some cases, the partial pressures are given and you need to calculate the mole fraction instead. It’s really just a matter of manipulating the equation to get the value of the unknown.

The partial pressure of oxygen can be calculated by simply multiplying the mole fraction of oxygen by the total pressure of the mixture. You first need to calculate the unitless mole fraction of oxygen, which we have already calculated based on the same units given in the previous sample problem, which is 0.21. Thus, plugging in the values, we get:

p(Oxygen) = 0.21 x 140kPap(Oxygen) = 29.4kPa

For more A level chemistry resources to help you revise and for information on studying chemistry A level, check out our A Level Chemistry Resources hub.